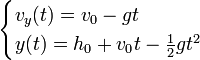calculo

miércoles, 21 de octubre de 2009

INTRODUCCIÓN

Con el siguiente informe describimos la experiencia adquirida en el laboratorio al poner en practica lo estudiado teóricamente y mostramos de una forma clara y resumida los métodos utilizados en nuestro experimento.

También dimos de una forma explícita el desarollo de los conceptos como son velocidad, distancia y gravedad que influenciaron en nuestro trabajo.

Dicho informe es una representación sencilla de ciertos fenómenos analizados por Galileo.

OBJETIVOS

Estudiar los conceptos básicos del movimiento parabólico descrito en la experiencia realizada en el laboratorio.

Describir las características del movimiento parabólico que realiza el balín.

Desarrollar los conceptos de velocidad, distancia y gravedad descritos por el movimiento y la distancia del balín al ser lanzados hacia distancias cada vez mayores.

Analizar por medio de los datos el movimiento y determinar su comportamiento con respecto al plano coordenado (abscisa x, ordenada y)

Movimiento Parabolico

Supondremos que el proyectil parte del origen con una velocidad V₀ que forma un ángulo θo con la horizontal. Las componentes iniciales de la velocidad son V₀x = V_o cosθ₀ ; V_oy = V₀ senθ₀.

Sustituyendo estas expresiones en las ecuaciones anteriores, se obtienen las ecuaciones cinemáticas del movimiento de un proyectil:

ax = 0

ay = - g

Vx = V_o cosθ_o

Vy = - gt + V_o senθ_o

x = V_o cosθ_o t

y = - ½ g t² + V_o senθ_o t

Las preguntas que pueden surgir son:

¿Cuál es la trayectoria del proyectil?

De las ecuaciones paramétricas X y Y, eliminemos el tiempo:

Tenemos una ecuación de la forma: y = - ax²+bx , que es la ecuación de una parábola.

b) ¿Cuál es la velocidad del proyectil en un momento dado?

Por el teorema de Pitágoras, la magnitud es: v = V²x + V²y , y el ángulo que forma con la horizontal es:

Propiedades y características

La velocidad media siempre tiene el mismo valor, con independencia del intervalo de tiempo elegido. En consecuencia, las velocidades instantánea y media coinciden.

La distancia recorrida se calcula multiplicando la magnitud de la velocidad (celeridad o rapidez) por el tiempo transcurrido. Esta operación también puede ser utilizada si la trayectoria del cuerpo no es rectilínea, pero con la condición de que la celeridad o módulo de la velocidad sea constante.

La celeridad puede ser nula (reposo) positiva o negativa. Por lo tanto el movimiento puede considerarse en dos sentidos; una celeridad negativa representa un movimiento en dirección contraria al sentido que convencionalmente hallamos adoptado como positivo.

De acuerdo con la Primera Ley de Newton, toda partícula permanece en reposo o en movimiento rectilíneo uniforme cuando no hay una fuerza neta que actúe sobre el cuerpo. Esta es una situación ideal, ya que siempre existen fuerzas que tienden a alterar el movimiento de las partículas, por lo que el movimiento rectilíneo uniforme es dificil de encontrar.

Ecuaciones del movimiento.

Sabemos que la velocidad $v\,$ es constante, esto es, no existe aceleración.

La posición $x\,$ en el instante $t\,$ viene dada por:

$x = x_0+vt\,$

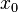donde $x_0\,$ es la posición inicial.

martes, 20 de octubre de 2009

Contenido

Ejercicios resueltos de Cinemática: Tiro vertical.

Resolver los siguientes problemas:

En todos los casos usar g = 10 m/s ².

Problema n° 1) Se lanza una pelota desde lo alto de un faro de 80 m de altura, con una velocidad inicial de 4 m/s hacia abajo.

a) ¿Cuánto tarda en llegar al suelo?.

b) ¿Con qué velocidad llega?.

c) ¿A qué altura está luego de 2 s de haberla arrojado?.

Ver solución del problema n° 1

Problema n° 2) Se lanza una piedra verticalmente hacia arriba con una velocidad de 250 m/s, determinar:

a) ¿Cuál es la velocidad a los 4 s?.

b) ¿Qué altura alcanzó en esos 4 s?.

c) ¿Cuánto tiempo tardará en alcanzar la altura máxima?.

Ver solución del problema n° 2

Problema n° 3) Determinar la velocidad inicial de un cuerpo lanzado hacia arriba y que alcanza una altura máxima de 48 m.

Ver solución del problema n° 3

Problema n° 4) Desde un puente se lanza una piedra verticalmente hacia abajo con una velocidad de 8 m/s, si la piedra tarda 2,5 s en llegar al agua, determinar:

a) ¿Con qué velocidad llega al agua?.

b) ¿Cuál es la altura del puente?.

Ver solución del problema n° 4

Responder el siguiente cuestionario:

Pregunta n° 1) ¿Qué entiende por aceleración de la gravedad?.

Ver respuesta a la pregunta n° 1

Pregunta n° 2) ¿La aceleración de la gravedad es un valor constante o variable?.

Ver respuesta a la pregunta n° 2

Pregunta n° 3) Qué velocidad posee un cuerpo cuando alcanza la altura máxima?.

Ver respuesta a la pregunta n° 3

Pregunta n° 4) ¿Dónde podría saltar más alto un atleta que practica salto en alto, en Tierra del Fuego o en Jujuy?

lunes, 19 de octubre de 2009

Video de movimiento parabolico!!*

miércoles, 14 de octubre de 2009

Movimieto Rectilino Uniforme

Las gráficas en el MRU

Un movimiento rectilíneo uniforme es aquel en el que la trayectoria es una línea recta y su velocidad es constante.

El movimiento del coche por la carretera que estudiamos en el ejercicio del dossier La velocidad es un caso claro de movimiento rectilíneo uniforme.

Para conocer el espacio recorrido en un MRU basta con despejar s de la expresión de la velocidad:

$v = \frac{s}{t} \to s = v \cdot t$

En un MRU el espacio recorrido, s, es igual a la posición final, x, menos la posición inicial, x₀:

s = x - x₀ = v · t → x = x₀ + v · t

Las siguientes gráficas posición-tiempo representan dos casos de movimientos rectilíneos uniformes.

Imagen:

Gráfica partiendo del origen

El móvil parte del origen y se aleja de él a una velocidad constante de 5m/s. La gráfica es una recta ascendente. Como X₀= 0, la posición del móvil, en cada instante será: X = 5 . t.

Imagen:

Gráfica partiendo de un punto situado a una cierta distancia del origen

El móvil parte de un punto situado a 80 m del origen y se aproxima a él a 10m/s. La gráfica es una recta descendente. Como X₀= 80 m, la posición, en cada instante, será: x = 80 - 10t.

La caída libre

La caída libre como sistema de referencia

Un sistema de referencia ligado a un cuerpo en caída libre puede considerarse inercial o no inercial en función del marco teórico que esté utilizándose.

En la física clásica, la gravedad es una fuerza que aparece sobre una masa y que es proporcional al campo gravitatorio medido en la posición espacial donde se encuentre dicha masa. La constante de proporcionalidad es precisamente el valor de la masa inercial del cuerpo, tal y como establece el principio de equivalencia. En la física relativista, la gravedad es el efecto que produce sobre las trayectorias de los cuerpos la curvatura del espacio-tiempo; en este caso, la gravedad no es una fuerza, sino una geodésica. Por tanto, desde el punto de vista de la física clásica, un sistema de referencia en caída libre es un sistema acelerado por la fuerza de la gravedad y, como tal, es no inercial. Por el contrario, desde el punto de vista de la física relativista, el mismo sistema de referencia es inercial, pues aunque está acelerado en el espacio, no está acelerado en el espacio-tiempo. La diferencia radica en la propia definición de los conceptos geométricos y cinemáticos, que para un marco teórico y para el otro, son completamente diferentes.

Aceleración en caída libre

En este movimiento se desprecia el rozamiento del cuerpo con el aire, es decir, se estudia en el vacío. El movimiento de la caída libre es un movimiento uniformemente acelerado. La aceleración instantánea debida sólo a la gravedad es independiente de la masa del cuerpo, es decir, si dejamos caer un coche y una pluma, ambos cuerpos tendrán la misma aceleración, que coincide con la aceleración de la gravedad ('g').

Cuando la caída libre tiene lugar en el seno de un fluido como el aire, hay que considerar las fuerzas viscosas que actúan sobre el cuerpo. Aunque técnicamente la caída ya no es libre, desarrollaremos en adelante las ecuaciones incluyendo el término aerodinámico excepto en los casos en los que no proceda (p.e. espacio exterior).

Caída libre totalmente vertical

El movimiento del cuerpo en caída libre es vertical con velocidad creciente (aproximadamente movimiento uniformemente acelerado con aceleración g) (aproximadamente porque la aceleración aumenta cuando el objeto disminuye en altura, en la mayoría de los casos la variación es despreciable). La ecuación de movimiento se puede escribir en términos la altura y:

(1) $ma_y = m\frac{d^2y}{dt^2} = -mg + F_r(v_y)$

Donde:

$a_y, v_y\;$ , son la aceleración y la velocidad verticales.

$F_r\;$ , es la fuerza de rozamiento fluidodinámica (que es creciente con la velocidad).

Si se desprecia en una primera aproximación la fuerza de rozamiento, cosa que puede hacerse para caídas desde pequeñas alturas de cuerpos relativamente compactos, en las que se alcanzan pequeñas velocidades la solución de la ecuación diferencial (1) para las velocidades y la altura vienen dada por:

$\begin{cases} v_y(t)= v_0 - gt \\ y(t) = h_0 + v_0t -\frac{1}{2}gt^2 \end{cases}$

Donde v₀ es la velocidad inicial, para una caída desde el reposo v₀ = 0 y h₀ es la altura inicial de caída.

Para grandes alturas u objetos de gran superficie (una pluma, un paracaídas) es necesario tener en cuenta la fricción del aire que suele ser modelizada como una fuerza proporcional a la velocidad, siendo la constante de proporcionalidad el llamado rozamiento aerodinámico k_w:

(2) $ma_y = m\frac{d^2y}{dt^2} = -mg - k_wv_y$

En este caso la variación con el tiempo de la velocidad y el espacio recorrido vienen dados por la solución de la ecuación diferencial (2):

$\begin{cases} v_y(t)= v_0e^{-k_wt/m} + \cfrac{mg}{k_w}(e^{-k_wt/m}-1)\\ y(t) = h_0 - \cfrac{mgt}{k_w}+m\left(\cfrac{mg+k_wv_0}{k_w^2}\right)(e^{-k_wt/m}-1) \end{cases}$

Nótese que en este caso existe una velocidad límite dada por el rozamiento aerodinámico y la masa del cuerpo que cae:

$v_\infty = \lim_{t\to \infty} v_y(t) = -\frac{mg}{k_w}$

Movimiento Parabolico.

El movimiento parabólico es de caída libre en un marco de referencia móvil. Sin tener en cuenta la resistencia del aire, la componente horizontal de la velocidad de un proyectil permanece constante, mientras su componente vertical independientemente esta sujeta a una aceleración constante hacia abajo.

Utilizando el movimiento parabólico realizado en el laboratorio como ejemplo hemos aprendido como armar modelos para resolver problemas de cinemática.

MOVIMIENTO PARABÓLICO

Sustituyendo estas expresiones en las ecuaciones anteriores, se obtienen las ecuaciones cinemáticas del movimiento de un proyectil:

ax = 0

ay = - g

Vx = V_o cosθ_o

Vy = - gt + V_o senθ_o
x = V_o cosθ_o t

y = - ½ g t² + V_o senθ_o t

Las preguntas que pueden surgir son:

¿Cuál es la trayectoria del proyectil?

De las ecuaciones paramétricas X y Y, eliminemos el tiempo:

Tenemos una ecuación de la forma: y = - ax²+bx , que es la ecuación de una parábola.

b) ¿Cuál es la velocidad del proyectil en un momento dado?

Por el teorema de Pitágoras, la magnitud es: v = V²x + V²y , y el ángulo que forma con la horizontal es:

c) ¿Cuál es su máxima altura?

Esto sucede cuando su velocidad vertical se anula:

Vy = 0 = - g t + Vo senθ.

De aquí se despeja el tiempo:

t = V_o senθ_o

Y lo llevamos a la ecuación que nos da la ordenada y, que llamamos ahora

La altura máxima Y.

Y = V²_o sen²θ_o

¿Cuál es el alcance?

Es el valor de x cuando el proyectil ha llegado al suelo, es decir, para y=0; esto nos da:

0 = - ½ g t ² + Vo senθ_o t = ( - ½ g t + Vo senθ_o ) t:

t = 2V_o senθ_o_

Y lo llevamos a la ecuación de x, que llamamos ahora el alcance de x.

X = V_o cosθ_o 2V_o senθ_o_

Y como sabemos que 2cosθo senθo = sen2θo, se tiene:

X = V²_o_ sen2θ_o

¿Para qué valor del ángulo inicial θo el alcance es máximo?

El alcance es máximo cuando sen2θo es máximo, es decir, cuando sen2θo = 1. Por lo tanto, el ángulo 2θo es igual a 90° y θo es igual a 45°.

Si el proyectil es lanzado horizontalmente, con velocidad Vo desde el origen, las ecuaciones cinemáticas se simplifican y se obtiene:

ax = 0 ay = -g
Vy = V₀ V_y = -g t
x = V₀ t y = - ½ g t ²

Estas ecuaciones se simplifican aun más si se toma el eje y hacia abajo. En este caso, g es positiva y las ecuaciones se escriben:

ax = 0 ay = g
Vy = V_o Vy = g t
x = V_o t y = ½ g t ²